Imagine you have a string, and you need to break it into parts such that each part is a palindrome. Sounds interesting, right? This concept is known as palindrome partitioning. Palindrome partitioning is the process of breaking a string into palindromic substrings. Discover how to implement this in programming with our comprehensive guide and code examples.
Welcome back, aspiring interview champions! In this article, we’ll dive into palindrome partitioning, discuss its importance for coding interviews, and show you how to implement it effectively in C# using a backtracking approach. Prepare to enhance your problem-solving skills and ace your next technical interview!
FREE : If you’re a new visitor preparing for an interview and need help or want to request a new question, you can use the form on the right side to ask your question. It’s free and doesn’t require signing in. Alternatively, you can ask in our Quora space, which is also free, and you’ll receive a response within 24 hours. Go ahead and check it out! do check Find the largest sum subarray using Kadane’s Algorithm ,Mastering Object-Oriented Programming in C++, Palindrome Partitioning A Comprehensive Guide , Method Overloading vs. Method Overriding in C#
Table of Contents
What is Palindrome String With Example
A palindrome is a sequence of characters that reads the same forwards and backwards. For instance, “radar” and “level” are palindromes. They maintain their original form even when reversed. This property makes them intriguing and often used in wordplay and puzzles.
In programming, identifying palindromes is a common task, aiding in tasks like string manipulation and pattern matching. Remember, a palindrome retains its symmetry regardless of orientation. So, the next time you encounter a string, consider whether it might be a palindrome!
What is Palindrome Partitioning
I believe that you have read above section where I have described what is palindrome string therefore let’s dive in to it. Palindrome partitioning involves splitting a string into substrings, where each substring is a palindrome (a sequence that reads the same forwards and backwards). For instance, given the string “aab”, possible palindrome partitions are [“a”, “a”, “b”] and [“aa”, “b”].
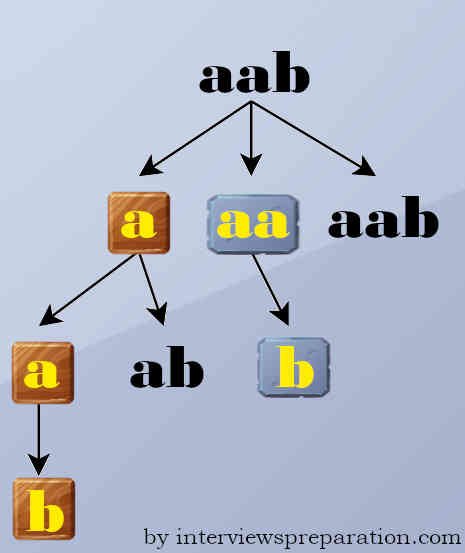
Importance Of Palindrome Partitioning
Understanding palindrome partitioning is crucial in fields like computational biology, data compression, and cryptography. It helps in optimizing algorithms that deal with string manipulations and pattern matching.
Backtracking Algorithm Explained
Ever heard of backtracking? Backtracking Algorithm a problem-solving approach where we explore all options and discard those that don’t meet the problem’s criteria. In the realm of palindrome partitioning, here’s how it works:
- Start from the beginning of the string.
- Incrementally partition the string and check if each partition is a palindrome.
- If a partition is a palindrome, we recursively partition the remaining substring.
We’ll bring theory to life with practical code examples. Stay tuned! let’s dive into coding! In the next section
Implementing Palindrome Partitioning in C#
using System;
using System.Collections.Generic;
public class Solution {
public IList<IList<string>> Partition(string s) {
var result = new List<IList<string>>();
Backtrack(s, 0, new List<string>(), result);
return result;
}
// to understand below funcation check explanation part named 'How Backtrack Works '
private void Backtrack(string s, int start, List<string> path, List<IList<string>> result)
{
if (start == s.Length) {
result.Add(new List<string>(path));
return;
}
for (int end = start + 1; end <= s.Length; end++) {
if (IsPalindrome(s, start, end - 1)) {
path.Add(s.Substring(start, end - start));
Backtrack(s, end, path, result);
path.RemoveAt(path.Count - 1);
}
}
}
// to understand below funcation check explanation part named 'Find Palindrome String in C#'
private bool IsPalindrome(string s, int left, int right) {
while (left < right) {
if (s[left] != s[right]) {
return false;
}
left++;
right--;
}
return true;
}
}
I know you may have many questions regarding the above code, but fret not. I have covered each code block in the upcoming sections.
Find Palindrome String in C#
Have you been able to locate the code for finding palindrome numbers? As the name suggests, we will first explain the ‘IsPalindrome’ method. This function assists us in identifying palindrome strings.
Suppose we have the string “level” and initially, left points to the first character (‘l’) and right points to the last character (‘l’). We compare both characters and find them equal. Then, we increment left and decrement right, so left now points to the second character (‘e’) and right points to the second-last character (‘e’). This process continues until left becomes greater than or equal to right. If all comparisons are successful, the function returns true, indicating that “level” is a palindrome.
How Backtrack Works
Keep your focus here as we delve into explaining the backtracking logic. Now, let’s dissect the code.
private void Backtrack(string s, int start, List path, List> result): This line defines a method named Backtrack, which takes four arguments: the string s, an integer start, a list of strings path, and a list of lists of strings result.
if (start == s.Length) { result.Add(new List(path)); return; }: This block of code checks if we have reached the end of the string ‘s’. If so, it means we have found a valid partition, so we add the current path to the result list and return.
for (int end = start + 1; end <= s.Length; end++) { }: Here, we iterate over possible end indices starting from start + 1 to s.Length. This loop represents our exploration of different partition sizes.
if (IsPalindrome(s, start, end – 1)) { path.Add(s.Substring(start, end – start)); Backtrack(s, end, path, result); path.RemoveAt(path.Count – 1); }: Within the loop, we check if the substring from start to end – 1 is a palindrome using the IsPalindrome method. If it is, we add this substring to the current path, recursively call Backtrack with the new starting index end, and then remove the last added substring from path.
Adopting the backtracking algorithm may pose a challenge, but I encourage you to try these codes yourself and keep practising. Practising algorithms is crucial for mastery. If you encounter difficulties, fret not. In the next section, I’ll provide examples to help you visualize both the problem and its solutions.
Visualizing the Algorithm
Stay with us I will upload video soon alternatively subscribe to get notification it is free.
Practical Application
Case Studies
Imagine you’re developing a text editor with a feature to highlight palindromic substrings. By implementing the palindrome partitioning algorithm, you can efficiently identify and highlight these substrings.
Common Challenges
Performance: Backtracking can be computationally expensive for large strings.
Edge Cases: Handling strings with no palindromes.
Solutions
Optimization: Use dynamic programming to store results of palindrome checks.
Preprocessing: Validate input to handle edge cases upfront.
Summarizing Palindrome Partitioning Guide
In this comprehensive guide, we explored the fascinating concept of palindrome partitioning and its significance, particularly for aspiring programmers preparing for technical interviews. We began by understanding the theory behind palindrome partitioning and delved into its practical implementation using C#. Through a detailed breakdown of the IsPalindrome and Backtrack methods, we deciphered the intricate logic behind identifying palindromic substrings and recursively partitioning strings. Despite the initial complexity, we encouraged readers to engage with the code examples, emphasizing the importance of practice in mastering algorithms.